Every now and then, however, I get a flash of insight that seems to put the nature of reality just nearly within my grasp. The feeling is brief and tantalizing, like trying to recall the details of a dream as they evaporate on waking. But it’s thrilling.
My latest one came while pondering the odd fact that there is no discernible difference between gravity and the acceleration due to motion.
When you’re sitting in a parked car, there is a force pressing your butt down into the seat. That’s gravity acting on your mass. (I’ll refrain from making comments about the mass of your butt.) When you peel out of that parking space and go from zero to sixty in 6.2 seconds, there is another force pressing your back against the seat. That’s acceleration. Science says that if you didn’t already know which force was acting on you, and the only clue you had was how it felt (not how it looks out the window, not the roar of the engine, not that you remember the Earth being beneath your feet when you got into the car, etc.), you couldn’t tell whether you were sitting still in a gravity field or accelerating through space, or some combination of both.
This turns out to be useful for sending humans on long interplanetary journeys in the future. If we invent a propulsion system that can sustain enough power continuously, then the spaceship can accelerate at 1g halfway to its destination, then turn around and decelerate (which is just accelerating in the other direction) at 1g the rest of the way. The humans on board will avoid the many health hazards of prolonged weightlessness; they’ll experience “gravity” holding them to the spaceship’s floors.
But what accounts for the fact that gravity and acceleration are the same thing? When you’re accelerating, your velocity is changing from moment to moment. And your velocity is nothing more than a measure of how your position changes from moment to moment. If your velocity is constant, you experience no acceleration. That is, you can be changing your position, but as long as it changes at a steady rate, you’re not accelerating. On the other hand, as soon as there is a change in the rate at which your position changes, the force due to acceleration appears.
- Velocity: rate of change of position
- Acceleration: rate of change of velocity
You can have lots of velocity and still have zero acceleration. If you plot your position over time on a graph, anything that’s a straight line means your velocity is constant and you’re not accelerating. To get acceleration, the graph needs to curve. (Any curve will do, but if the acceleration happens to be constant, then the curve is a parabola.)
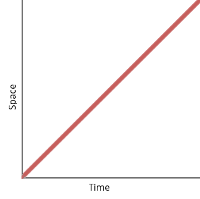
Unchanging velocity; no acceleration, no force.
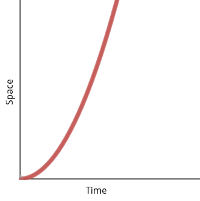
Velocity changing at a constant rate; produces a parabolic curve and a steady force.
Wrap your head around this
Here’s another recent insight that might help you to understand the idea of spacetime: The Big Bang happened in this very spot 13.8 billion years ago, and it’s also happening right now, 13.8 billion light-years away in every direction.
When you’re standing still on the ground and experiencing the pull of the Earth’s gravity, what’s changing to make that feel like acceleration? Not your position (with respect to the Earth). Not the rate of change of your position. But time is passing, and thanks to Dr. Einstein we know that space and time are mysteriously bundled together into something called spacetime. So even if you’re not moving through space, you’re always moving through spacetime.
But as I pointed out above, it’s not enough to be moving to experience acceleration. The rate at which you’re moving must itself be changing. When you’re standing still on the Earth, you’re moving through spacetime, yes; but the rate at which you’re moving through spacetime stays the same. So again: what’s changing that can give rise to a force like acceleration?
Standing still in space…
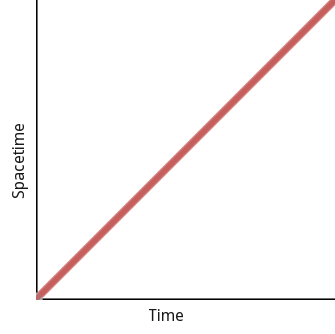
…is still moving through spacetime.
Well, hang on. We know (also from Einstein) that the presence of a large mass like the Earth causes spacetime to curve — whatever that means. So maybe it’s wrong to draw our spacetime axis as a straight line.
Suppose spacetime happens to curve just like this:
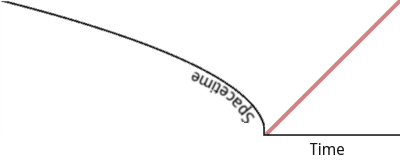
Standing still in curved spacetime.
Straightening the axis again forces the plot into a curve. (In fact, in this [manufactured] case it forces it into the shape of our old friend the parabola.)
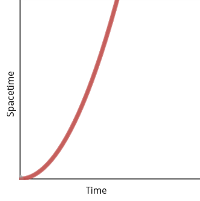
Standing still in curved spacetime.
So. I’ve managed to convince myself that just standing still in a region of curved spacetime can look exactly like accelerating in a region of flat spacetime. Spacetime itself remains a difficult idea to internalize, to say nothing of it being curved, and even if I’ve managed to make one graph look like another in a hand-wavy way, still none of it makes any intuitive sense.
But I observe that moving at a constant velocity requires no energy. You need energy to change your velocity — i.e., to accelerate. And you need mass to curve spacetime. And as we know (thank you once again, Dr. Einstein), energy and mass are the same. Somehow it’s all down to the interactions between space, time, and energy. But what are they?
See what I mean? I can almost feel what real understanding would be like. It’s maddening.
[Update: followup thoughts added here.]
My head hurts!
But you get a standing ovation anyway!